
Safe and Uncertainty-Aware Learning
Research Question
How can we predict and react to rare but potentially disastrous events?
Summary
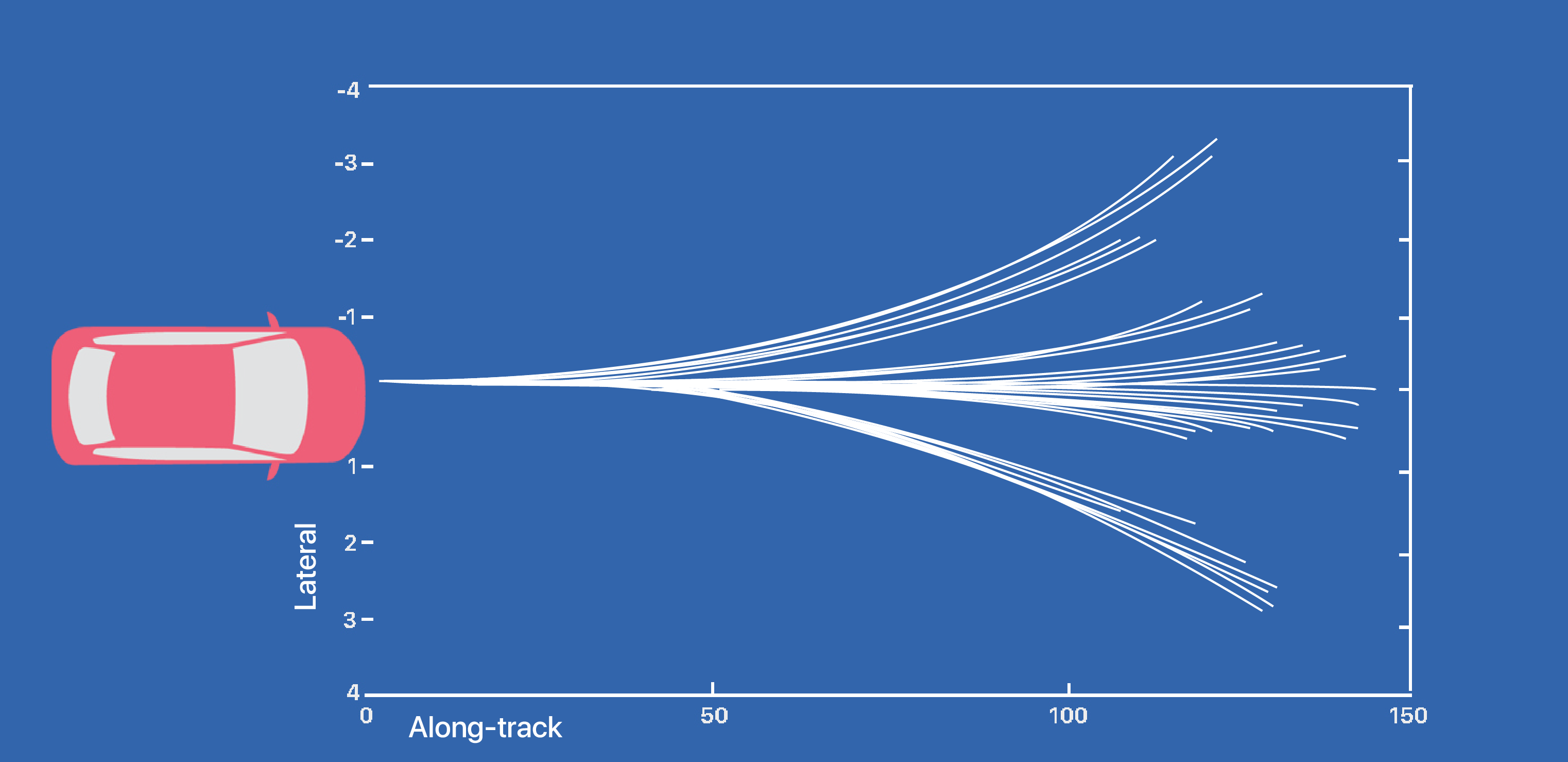
Theoretical foundations of risk-sensitive decision-making and learning. Deployment of safety-critical systems in uncertain environments requires predicting and reacting to rare but potentially disastrous event. Our group focuses on devising risk-sensitive algorithms for various types of real world scenarios. This includes projects to devise algorithms for risk-sensitive planning, for inferring the profile of a risk-sensitive expert (e.g., inverse reinforcement learning, imitation learning), for interactive decision making for self-driving cars (e.g., for traffic weaving scenarios), for safe transfer of control policies from simulation environments to the real world (e.g., autonomous driving in varying weather conditions), and new techniques to merge formal methods with stochastic optimal control and deep learning for high-confidence implementation on safety-critical systems.
Related Works
-
J. Harrison, A. Sharma, and M. Pavone, “Meta-Learning Priors for Efficient Online Bayesian Regression,” in Workshop on Algorithmic Foundations of Robotics, Merida, Mexico, 2018. (In Press)
Abstract: Gaussian Process (GP) regression has seen widespread use in robotics due to its generality, simplicity of use, and the utility of Bayesian predictions. In particular, the predominant implementation of GP regression is kernel-based, as it enables fitting of arbitrary nonlinear functions by leveraging kernel functions as infinite-dimensional features. While incorporating prior information has the potential to drastically improve data efficiency of kernel-based GP regression, expressing complex priors through the choice of kernel function and associated hyperparameters is often challenging and unintuitive. Furthermore, the computational complexity of kernel-based GP regression scales poorly with the number of samples, limiting its application in regimes where a large amount of data is available. In this work, we propose ALPaCA, an algorithm for efficient Bayesian regression which addresses these issues. ALPaCA uses a dataset of sample functions to learn a domain-specific, finite-dimensional feature encoding, as well as a prior over the associated weights, such that Bayesian linear regression in this feature space yields accurate online predictions of the posterior density. These features are neural networks, which are trained via a meta-learning approach. ALPaCA extracts all prior information from the dataset, rather than relying on the choice of arbitrary, restrictive kernel hyperparameters. Furthermore, it substantially reduces sample complexity, and allows scaling to large systems. We investigate the performance of ALPaCA on two simple regression problems, two simulated robotic systems, and on a lane-change driving task performed by humans. We find our approach outperforms kernel-based GP regression, as well as state of the art meta-learning approaches, thereby providing a promising plug-in tool for many regression tasks in robotics where scalability and data-efficiency are important.
@inproceedings{HarrisonSharmaEtAl2018, author = {Harrison, J. and Sharma, A. and Pavone, M.}, title = {Meta-Learning Priors for Efficient Online Bayesian Regression}, booktitle = {{Workshop on Algorithmic Foundations of Robotics}}, year = {2018}, note = {In press}, address = {Merida, Mexico}, month = oct, url = {https://arxiv.org/pdf/1807.08912.pdf}, keywords = {press}, owner = {apoorva}, timestamp = {2018-10-07} } -
S. Singh, J. Lacotte, A. Majumdar, and M. Pavone, “Risk-sensitive Inverse Reinforcement Learning via Semi- and Non-Parametric Methods,” Int. Journal of Robotics Research, 2018. (In Press)
Abstract: The literature on Inverse Reinforcement Learning (IRL) typically assumes that humans take actions in order to minimize the expected value of a cost function, i.e., that humans are risk neutral. Yet, in practice, humans are often far from being risk neutral. To fill this gap, the objective of this paper is to devise a framework for risk-sensitive IRL in order to explicitly account for a human’s risk sensitivity. To this end, we propose a flexible class of models based on coherent risk measures, which allow us to capture an entire spectrum of risk preferences from risk-neutral to worst-case. We propose efficient non-parametric algorithms based on linear programming and semi-parametric algorithms based on maximum likelihood for inferring a human’s underlying risk measure and cost function for a rich class of static and dynamic decision-making settings. The resulting approach is demonstrated on a simulated driving game with ten human participants. Our method is able to infer and mimic a wide range of qualitatively different driving styles from highly risk-averse to risk-neutral in a data-efficient manner. Moreover, comparisons of the Risk-Sensitive (RS) IRL approach with a risk-neutral model show that the RS-IRL framework more accurately captures observed participant behavior both qualitatively and quantitatively, especially in scenarios where catastrophic outcomes such as collisions can occur.
@article{SinghLacotteEtAl2018, author = {Singh, S. and Lacotte, J. and Majumdar, A. and Pavone, M.}, title = {Risk-sensitive Inverse Reinforcement Learning via Semi- and Non-Parametric Methods}, journal = {{Int. Journal of Robotics Research}}, year = {2018}, note = {In Press}, url = {https://arxiv.org/pdf/1711.10055.pdf}, keywords = {press}, owner = {ssingh19}, timestamp = {2018-03-30} }